1. Folytonos-determinisztikus elorejelzés
A folytonos változók elorejelzésére jó példa a homérséklet-elorejelzés. A legegyszerubb ábrázolási metódus az ún. scatter-plot, ahol két dimenzióban felrakjuk az összetartozó elorejelzés-megfigyelés pontokat.
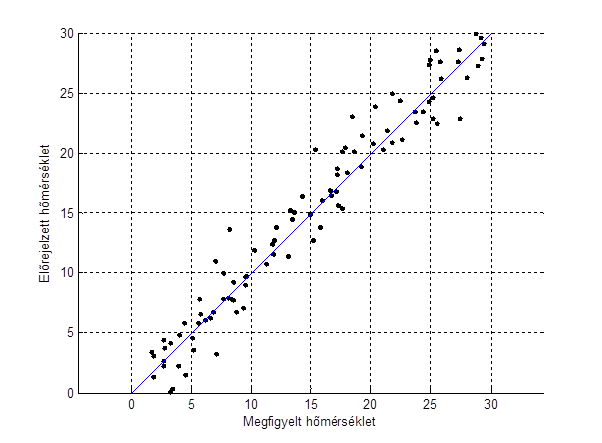
Az ideális elorejelzés az lenne, ha az összes pont a kék, átlós egyenesen helyezkedne el.
Ha számszerusíteni szeretnénk az elorejelzés hibáját, akkor valahogyan ettol az egyenestol való eltérést kell figyelembe vennünk. Több méroszám létezik ennek leírására:
- Átlagos hiba (mean error/bias):
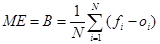[1]
ahol fi az i. elorejelzett érték, az oi pedig i. megfigyelt érték.
Értéktartomány: -8..+8
Tökéletes elorejelzés esetén értéke: 0
Ez a legegyszerubb méroszám, viszont több hátránya is van: Nem méri a hiba abszolút értékét, és az elorejelzés-megfigyelés közötti megfelelést: a nullát úgy is el lehet érni, hogy pozitív-negatív irányban kikompenzálják egymást a hibák.
- Átlagos abszolút hiba (mean absolute error):
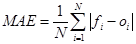[2]
Értéktartomány: 0..+8
Tökéletes elorejelzés esetén értéke: 0
Az elozohöz képest itt a hibák abszolút értékét vesszük. Hátránya, hogy nem veszi figyelembe a hiba irányát.
- Átlagos négyzetes hiba (mean squared error):
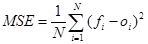[3]
Ez sem veszi figyelembe a hiba irányát, és a nagy eltérésekre érzékenyebb a négyzetre emelés miatt.
- Átlagos négyzetes hiba gyöke (root mean squared error):
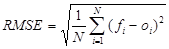[4]
Ez az elozo kifejezés (MSE) négyzetgyökeként értelmezheto, és az eredeti mennyiséggel (azaz a megfigyelt változóval) azonos mértékegységgel rendelkezik.
- Korrelációs együttható
Az érthetoség és az egyszerubb felírás érdekében érdemes eloször bevezetni az átlagot és a szórást. Az elorejelzések és megfigyelések átlaga: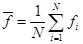
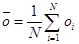
A szórások definíciója elorejelzésre és megfigyelésre:
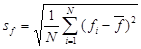[5]
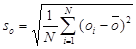[6]
Ezekkel a mennyiségekkel a korrelációs együttható kifejezése:
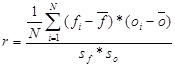[7]
Értéktartomány: -1..+1
Tökéletes elorejelzés esetén értéke: 1
Ez a szám azt mondja meg, hogy a pontokat 2 dimenzióban felrajzolva mennyire vagyunk közel egy egyeneshez (nem feltétlenül a 45 fokos "tökéletes" egyeneshez!). Ennek következtében az eltolásra nem érzékeny (pl. ha az elorejelzett értékekhez hozzáadunk 10-et, ugyanazt az értéket kapjuk). Emellett érzékeny a kiugró adatokra.
Megjegyzés: Ezt a képletet bináris elorejelzésekre alkalmazva az ott tárgyalt MCC-t (Matthews correlation coefficient) kapjuk.
- Lineáris regresszió meredeksége: Ez annak az egyenesnek a meredeksége, amit a ponthalmazra ráilleszthetünk.
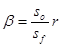[8]
Az 1 jelenti a tökéletes elorejelzést, azaz egy 45 fokos egyenest. Viszont ez az egyenes nem feltétlenül egyezik meg az y=x egyenessel. Ebben a képletben az s0 a megfigyelt értékek szórása, sf az elorejelzések szórása, és r a korrelációs együttható. Ezen mennyiségek a fentiekben vannak definiálva ([5], [6], [7]).
- Skill-score: Természetesen ez a fajta általánosított méroszám folytonos elorejelzésekre is alkalmazható, nem csak binárisokra.
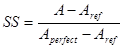[9]
Itt az Aref a referencia elorejelzés pontszámát jelöli. A referencia elorejelzés általában a klimatológiát vagy a perzisztencia elorejelzést jelenti. Az elobbinek két fajtája van, az egyiknél az adatok átlagát használjuk fel, a másiknál pedig egy más forrásból vett idosorok adatának átlagát vesszük (pl. adott napon, hónapban, attol függoen, milyen idopontra vonatkozik az elorejelzés). Perzisztencia elorejelzés esetén az idojárás utolsó észlelt állapototát vetítjük ki a jövore, és azt jelezzük elore, változatlanságot feltételezve.
Az Aperfect a tökéletes elorejelzés pontszámát jelenti.
Tekintsünk a fenti folytonos méroszámok jelentésének megvilágítására egy példát. A verifikálandó adathalmaz most az egyszeruség kedvéért 5 darab elorejelzés-megfigyelés párból áll.
| Elorejelzés | Megfigyelés | Hiba |
| 3 | 4 | -1 |
| 4 | 7 | -3 |
| 7 | 7 | 0 |
| 4 | 3 | 1 |
| 2 | 2 | 0 |
A hiba elojeles definíciója itt az elorejelzés mínusz a megfigyelés.
Az adatokat 2 dimenziós ábrán ábrázolva:
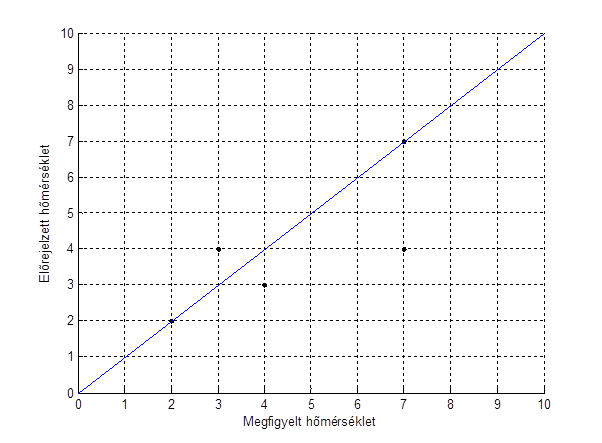
A fenti hibákból egyszeruen kiszámolhatóak a következo indexek:
- Átlagos hiba (ME) : -0.6
- Átlagos abszolút hiba (MAE): 1
- Átlagos négyzetes hiba (MSE): 2.2
- Átlagos négyzetes hiba gyöke (RMSE): 1.4832
- Elorejelzések átlaga: 4
- Megfigyelések átlaga: 4.6
A további, tárgyalt méroszámok értékei:
- Elorejelzések szórása: 1.6733
- Megfigyelések szórása: 2.0591
- Korrelációs együttható: 0.7546
- Lineáris regresszió meredeksége: 0.9286
Példa a skill-scorehez (SS): Ha az átlagos abszolút hibát (MAE) választjuk ki, és referencia értékének pl. a 0.5 fokot állítjuk be, akkor SS értéke a képletbe behelyettesítve -1, mivel a tökéletes elorejelzéshez nulla MAE érték tartozik. A -1-es érték azt jelenti, hogy a referenciánál 100%-kal rosszabb az elorejelzésünk.
Az MSE dekompozíciója
Az átlagos négyzetes hibának (MSE) többféle dekompozíciója létezik. Ezek azt a célt szolgálják, hogy meg tudjuk vizsgálni, a hiba milyen komponensekbol tevodik össze.
Egyik lehetséges felbontás, ami az átlagokat, szórásokat és a korrelációs együtthatót is felhasználja:
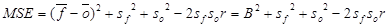[10]
A skill-score-t alkalmazva az MSE-re:
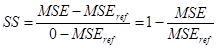[11]
Amennyiben a referencia elorejelzést a megfigyelések átlagának választjuk: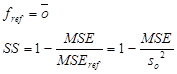
Ha MSE-re behelyettesítjük a fenti dekompozíciót: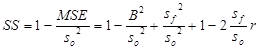
Ezt átalakítva a végleges alakja:
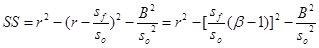[12]
Ebben három tagot lehet megkülönböztetni:
- lineáris asszociáció/megfelelés: azt fejezi ki, hogy a pontok mennyire esnek egy egyenesre. Ha 1, akkor az összes pont egy egyenesre esik. Ez a tag az ún. maximálisan megmagyarázott variancia.
- feltételes torzítás: a ponthalmaztra illesztett egyenesnek a 45 fokos meredekségtol való eltérését bünteti, ami azt jelenti, hogy ideális esetben nulla az értéke, egyébként pedig egy ettol eltéro pozitív értékkel rendelkezik.
- abszolút torzítás: az átlagos hibát (offszet) bünteti, ami annak a mértéke, hogy átlagos értelemben véve mennyivel vannak az elorejelzések és a megfigyelések egymástól eltolódva ([1] képlet).
Ha az SS mindhárom tagját megvizsgáljuk különbözo elorejelzések összehasonlítása során, akkor pontosabb képet kaphatunk.
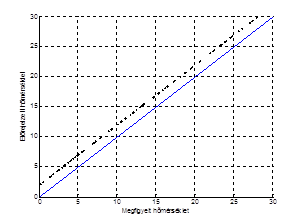
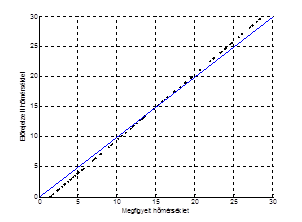
Példa: a következo két esetben a lineáris asszociáció értéke 1, azaz egy egyenes mentén fekszenek az adatok. Van viszont a bal oldali esetben abszolút torzítás (eltolás), a jobb oldali esetben pedig feltételes torzítás.
Egyéb méroszámok
- Anomália korreláció: A korrelációs együttható egy olyan módosításának felel meg, amikor az átlagos elorejelzés és az átlagos megfigyelés helyére a klimatológiai átlagot (c) helyettesítjük be:
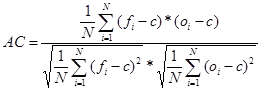[13]
Értéktartomány: -1..+1
Tökéletes elorejelzés esetén értéke: 1
Sok helyen használják numerikus elorejelzo modellek verifikációjához.
A folytonos elorejelzéseknél léteznek olyan méroszámok is, amelyek az elorejelzések és megfigyelések eloszlásainak különbségébol dolgoznak (pl. Linear error in probability space vagy LEPS). Ezeket itt nem tárgyalom.
2. Valószínuségi elorejelzés
Eloször is célszeru definiálni a valószínuségi eloszlásokat (ez a definíció csak diszkrét eseményekre vonatkozik, a folytonos változattal itt nem foglalkozom):
Valószínuségi elorejelzésrol akkor beszélünk, amikor egy esemény bekövetkezéséhez egy 0 és 1 közötti számot (vagy 0-100%) rendelünk hozzá, és ez az adott esemény valószínuségét reprezentálja.
Egy valószínuségi eloszlás abból áll, hogy az összes lehetséges kimenetelhez hozzárendelünk egy valószínuség értéket, olyan módon, hogy ezen számok összege 1.
A valószínuségi elorejelzés verifikációját abban az esetben érdemes elvégezni, ha viszonylag sok elorejelzés-megfigyelés pár áll a rendelkezésre. Például egyetlen bekövetkezett eseménybol, amit 80%-al jeleztünk elore - nem sok mindent lehet kijelenteni az elorejelzés jóságáról.
Kategóriákba sorolás: A valószínuségek bármilyen értéket felvehetnek 0 és 1 között. Verifikáció szempontjából viszont érdemes ezeket csoportosítani (például: 0-20%, 20-40%, 40-60%, 60-80%, 80-100%). Ezzel a kiértékelés sokkal átláthatóbbá, értelmezhetobbé válik. Lehetséges már az elorejelzést is úgy módosítani, hogy rögtön ezeket a kategóriákat jelezzük elore (pl. egy 76.343%-os érték bemondása helyett a 60-80%-os kategóriába soroljuk be).
A kiértékelésnél a tartományok középso értékei fognak számítani, ezért sokszor a kategóriákat is egybol ezen számokkal címkézik meg (ebben a példában: 10%, 30%, 50%, 70%, 90%). Megjegyzendo, hogy ezzel a lépéssel természetesen információveszteség keletkezik, viszont cserébe egyszerusítjük a kiértékelés folyamatát.
A valószínuségi elorejelzés tulajdonságai
- pontosság (accuracy): Ez annak a mértéke, hogy az elorejelzés és a megfigyelés mennyire egyezik meg. Ez az ún. Brier-scoreval mérheto.
- skill: Ez azt jelenti, hogy egy referencia elorejelzéshez (pl. klimatológia) képest mennyivel jobb az adott elorejelzés
- megbízhatóság (reliability): az elorejelzett valószínuségek közel vannak az esemény elofordulási gyakoriságához. Például, ha a kiértékelésnél az "50%-os valószínuség" címkéju kategóriát választjuk ki, és ebben a csoportban az elofordulási gyakoriság is pontosan 50%, akkor ebbol a szempontból tökéletesnek mondható az elorejelzésünk, legalábbis erre a kategóriára nézve.
- felbontás (resolution): különbözo elorejelzett valószínuségekhez különbözo esemény-gyakoriságok tartoznak. Pl. ha a 30%-os és a 70%-os valószínuségi kategóriában is közel ugyanakkora elofordulási gyakoriságot kapunk, az nem utal egy használható elorejelzésre - tehát nincs értelme megkülönböztetni a kategóriákat.
- élesség (sharpness): Arról ad információt, hogy az elorejelzés mennyire tér el a 0 és 1 szélsoértékektol. Ha mindig 0-át vagy 1-et jelzünk elore, akkor vagyunk a "legélesebbek", vagy más szóval a legbiztosabbak a kimenetelt illetoen. Az elorejelzési valószínuségek varianciájával mérheto.
- bizonytalanság (uncertainty): Ez az élességhez hasonló dolog, de itt az észlelést vizsgáljuk, hogy mennyire bizonytalan az adott esemény - a legbizonytalanabb eset az, ha a 50%-ban fordul elo. Az események varianciájával mérheto.
- diszkrimináció (discrimination): Mennyire lehet elkülöníteni az bekövetkezett eseményeket a nem bekövetkezett eseményektol úgy, hogy különbözo elorejelzési kategóriát adunk rájuk.
2.1 Bináris elorejelzés
Egy bináris esemény elorejelzéséhez tartozó valószínuségi eloszlás mindössze egyetlen számmal leírható, hiszen ha "x" a bekövetkezés valószínusége, akkor a nem bekövetkezés valószínusége (a komplementer esemény törvénye miatt) "1-x".
A megfigyelés ebben az esetben csak két értéket vehet fel: 0 vagy 1 (nem vagy igen).
Brier-score
A leggyakrabban alkalmazott méroszám. Megegyezik a folytonos elorejelzéseknél leírt MSE képletével (Mean Squared Error [3]), a különbség mindössze az, hogy az elorejelzés (f) egy 0 és 1 közötti szám, a megfigyelés (o) pedig csak 0 vagy 1 lehet.
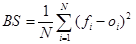[14]
A Brier-scorenak - hasonlóan az MSE-hez - többféle felbontása létezik. A legismertebb a megbízhatóság-felbontás-bizonytalanság felbontás. Ha az elorejelzések kategóriákba vanak sorolva, akkor felírható a következo alakban:
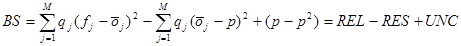[15]
Magyarázat:
M az elorejelzési kategóriák száma,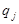 
a j. kategóriába eso elorejelzések elofordulási aránya, 
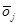az események elofordulási gyakorisága a j. kategóriában, p az esemény elofordulási aránya a teljes adathalmazon. Az 
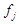az adott kategóriában elorejelzett (konstans) valószínuség.
A tagok értelmezése sorrendben:
- megbízhatóság (reliability): a kategóriákban elorejelzett valószínuségek mennyire térnek el a ténylegesen bekövetkezett gyakoriságoktól - mennyire jók az elorejelzett valószínuség értékek?
- felbontás (resolution): a kategóriákban tapasztalt gyakoriságok mennyire térnek el az átlagos gyakoriságtól (klimatológiától) - mennyire bontottuk fel jól kategóriákra az elorejelzést?
- bizonytalanság (uncertainty): Ez egyenlo az események varianciájával, azaz mennyire bizonytalan magának az eseménynek a bekövetkezése. Ez a tag nem függ az elorejelzéstol, csak az esemény elofordulásától/klimatológiájától.
Értéktartomány: 0..+1
Tökéletes elorejelzés esetén értéke: 0
A BS egyik hátránya, hogy ritka esemény esetén könnyu jó értékeket elérni. Az utolsó tag miatt különbözo adathalmazokon nincs értelme összehasonlítani a Brier-score-kat.
Brier skill score
A Brier-scorébol is lehet gyártani skill-score-t, a már megismert módszerrel:
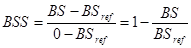[16]
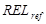és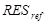 
is 0 lesz, és csak az utolsó "UNC" tag marad, ami viszont ugyanaz a referencia és a verifikált elorejelzésünk esetén. Ezért a fenti képlet leegyszerusödik:
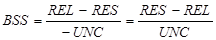[17]
Tökéletes elorejelzés esetén értéke: 1, a 0 jelenti azt, hogy nincs javulás a referencia elorejelzéshez képest. Hátránya, hogy kis adathalmaz esetén instabil értékeket ad, ritka eseménynél esetén (amikor p és UNC nulla közeli) sok adat kell, hogy megbízható értéket adjon.
Megbízhatósági diagram (reliability diagram)
Ez egy grafikus módszer, amivel egyszeruen lehet szemléltetni az elorejelzés megbízhatóságát, azaz a tényleges gyakoriság mennyire tér el az elorejelzettol. Emellett a Brier-score egyes tagjait is lehet vele vizuálisan szemléltetni.
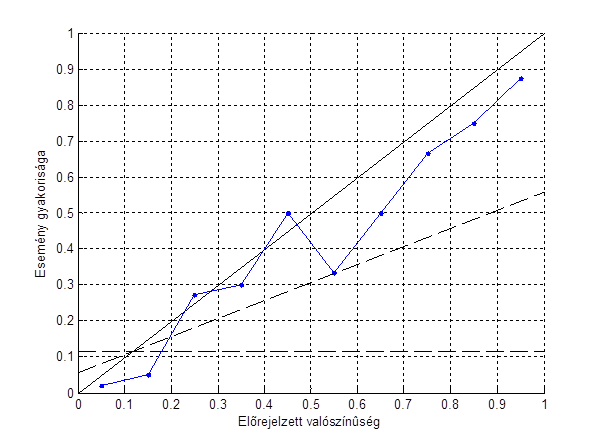
A vízszintes tengelyen az elorejelzett valószínuség, a függoleges tengelyen pedig az adott kategóriában az esemény elofordulási gyakorisága. Annál jobb az elorejelzés, minél jobban a foátló közelében van a kék görbe (ha a foátlón vagyunk, akkor REL=0). Amennyiben a kék görbe az átló alatt fut, akkor túlbecsültük, ha felette, akkor pedig alábecsültük az adott valószínuséget.
A vízszintes szaggatott vonal jelenti a klimatológiai elorejelzést, azaz ha mindig az esemény átlagos elofordulását jeleznénk elore (ez ebben a példában kb. 11%) - erre mondjuk, hogy nincs felbontása az elorejelzésnek (ezen a vonalon RES=0).
A foátló és a vízszintes között félúton elhelyezkedo szaggatott vonal pedig a BSS=0 értéket jelenti (REL=RES), e fölött BSS pozitív, alatta pedig negatív.
A megbízhatósági diagrammal rendszerint együtt szokták ábrázolni az úgynevezett élességi diagramot (sharpness diagram):
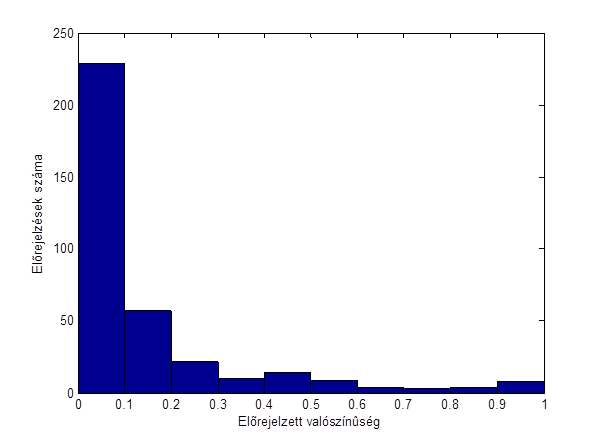
5. ábra
Diszkrimináció, ROC görbe
6. ábra
Ez hasonlít az élességi diagramra, viszont itt az egyes kategóriákban ketté vannak bontva az elorejelzések aszerint, hogy bekövetkezett-e vagy sem az adott esemény.
Tegyük fel, hogy a fenti adatok egy csapadék-elorejelzésre vonatkoznak, és egy tetofedo megkérdezi tolünk: "Ez rendben van, de milyen valószínuségi értéket javasolnak, ami felett nem érdemes elkezdeni a munkát."
Az ilyen jellegu kérdésre a ROC görbe adhat választ, amit a determinisztikus elorejelzéseknél már megemlítettem. Tulajdonképpen arról van szó, hogy M kategória esetén M-1 darab determinisztikus elorejelzéssé konvertáljuk a fenti valószínuségi elorejelzést a következo módon:
- "elvágjuk" a fenti ábrát két kategória között (10%, 20%, 30%-es stb. küszöbértékek mentén)
- meghatározzuk a hozzátartozó kontingencia-táblázatot (hit, miss, false alarm, correct negatives)
- kiszámoljuk a true positive rate (TPR) és false positive rate (FPR) értékeket, és ábrázoljuk egy diagramon. (a TPR és FPR részletes definícióit lásd az Elorejelzések verifikációja I. c. anyagban)
Az így kapott ábrát ROC görbének nevezzük:
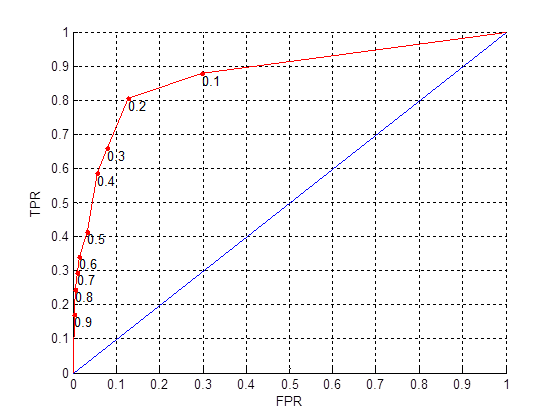
7. ábra
Így meg tudjuk állapítani az egyes valószínuségi küszöbértékekhez tartozó a TPR és FPR értékeket.
Kiválaszthatunk egyéb méroszámot is (pl. True Skill Statistic, Matthew's Correlation Coefficient), amelyhez aztán meghatározhatjuk az optimális döntési küszöbértéket is - az összes ponthoz tartozó érték kiszámolása után.
Mint méroszám, felhasználhatjuk a költség képletét is, amely a TPR és FPR értékekkel is felírható (a költség részletes kifejtését lásd az Elorejelzések verifikációja I. c. anyagban):
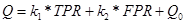
ROC görbe alatti terület
Amennyiben nem egy optimális küszöbértékre vagyunk kíváncsiak, hanem arra, hogy az adott valószínuségi elorejelzés potenciálisan milyen diszkriminációs képességgel rendelkezik, akkor e célból definiálhatjuk a ROC görbe alatti területet (az alábbi ábrán türkiz színnel van jelölve).
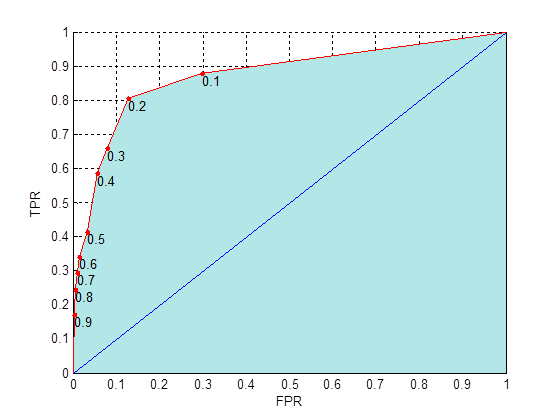
8. ábra
Általában kb. 0.7 felett tekintjük az elorejelzést gyakorlatban is hasznosnak. Összehasonlításképpen, a fenti ábrán ez a terület 0.874.
Meg kell említeni, hogy ritka események esetén a TPR-FPR pontok az ábra bal felére koncentrálódnak. Ha kevés minta áll rendelkezésre, akkor elofordulhat az is, hogy bizonyos értéknél nagyobb küszöbértékeket már nem tudunk ábrázolni - a magas valószínuségi kategóriákban nem lesz elég esetünk, hogy megállapítsuk ezeket az arányokat.
Fontos, hogy a ROC görbe a megbízhatóságról nem mond semmit, tehát egy nem korrekt valószínuségeket tartalmazó elorejelzés is lehet diszkriminatív. Ezért a megbízhatósági diagram és a ROC görbe együtt alkalmazandó, mivel mindketto más tulajdonságról ad információt.
2.2 Multikategóriás elorejelzés
Rank probability score
Amennyiben kettonél több elorejelzési kategória van, és ezek sorrendbe állíthatóak (pl. nincs eso, kevés eso, sok eso), akkor az ún. rank probability score-t (RPS) szokás használni. Ez a Brier-score egy általánosításának tekintheto, két kategória esetén meg is egyezik azzal.
A következo módon számolható: Képezni kell az elorejelzés és a megfigyelés diszkrét eloszlásfüggvényeit. (Az eloszlásfüggvény definíciója egy x értéknél: mi a valószínusége annak, hogy egy valószínuségi változó x-nél kisebb értéket vesz fel. Itt a "kisebb" alacsonyabb kategóriát jelent.)
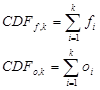[18]
Az f értékei a kategória valószínuségek (0 és 1 között), az o értékei pedig vagy 0 vagy 1 értéket vehetnek fel (indikátor változó - melyik kategória történt meg).
Ezt felhasználva a képlet, egyetlen esetre:
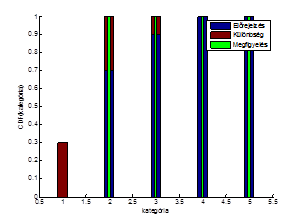
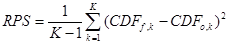[19]
ahol K a kategóriák száma.
Egy példa az értelmezés megkönnyítéséhez: Tegyük fel, hogy 5 kategóriát jelzük elore a következo valószínuségekkel: 30%, 40%, 20%, 10%, 0%. A bekövetkezett esemény a 2. kategóriába esik. Ezt egy ábrán szemléltetve:
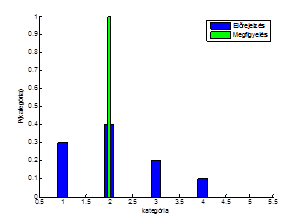
9. ábra
Az utolsó lépésben az összes esetre kiszámolt érték átlagát kell venni, így kapjuk a teljes verifikációs adathalmazra értelmezett RPS-t.
Értéktartománya megegyezik a Brier-score esetén látottakkal (0..+1) és tökéletes elorejelzés esetén értéke: 0. Akkor ad jó értéket, ha az elorejelzett valószínuség-eloszlás viszonylag éles, és a megtörtént esemény magas elorejelzett valószínuségu kategóriába esik.
Rank probability skill score
Ugyanúgy, ahogy a Brier-score esetén, itt is definiálható egy skill-score:
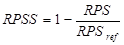[20]
ahol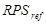 
egy referencia elorejelzés RPS értéke. Értkétartományára ugyanaz mondható el, mint a BSS-nél.
2.3 Folytonos elorejelzés
Continuous rank probability score
Az RPS-nek létezik egy kiterjesztése folytonos elorejelzésekre is, ez a CRPS:
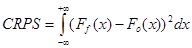[21]
Itt az összegzés helyett integrál található, és diszkrét eloszlásfüggvények helyett folytonosak szerepelnek: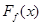 
az elorejelzés, 
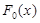a megfigyelések eloszlásfüggvénye.
Példa a szemléltetéshez: Ha az észlelés az x=3 pontban történt, az elorejelzés pedig egy 1 középpontú, 2 szórású Gauss görbe:
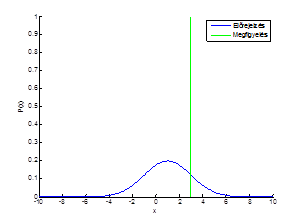
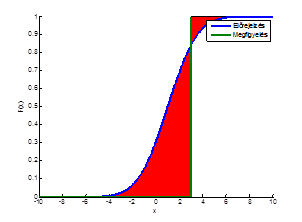
A teljes adathalmazra vett CRPS-t az összes esetre számolt átlaggal kapjuk meg.
A CRPS egy érdekes tulajdonsága, hogy amennyiben az elorejelzés determinisztikus, akkor megegyezik a folytonos elorejelzéseknél tárgyalt MAE méroszámmal (hiszen akkor a fenti integrál egy téglalap területébe megy át, aminek a magassága 1 egység hosszú, a másik oldalának hossza pedig az elorejelzés és a megfigyelés különbségének abszolút értéke).
Ez azért elonyös, mert így könnyen összehasonlíthatóvá válik egy determinisztikus és egy valószínuségi elorejelzés.
Rank histogram
Ez inkább egy diagnosztikai módszernek tekintheto, mint verifikációs módszernek. Ensemble elorejelzések esetén használják.
Az ensemble tagjainak összességét fel lehet fogni valószínuségi eloszlásként is, vagy annak jó közelítéseként.
Feltételezik, hogy az ensemble egyes tagjai egyenlo valószínuségekkel következnek be, ezért az egyes ensemble tagok közé nagyjából egyenlo számú megfigyelés kell essen.
Ha az ensemble N tagból áll, a tartományt felosztják N+1 részre (az ensemble elemei a tartományhatárok), és megnézik, hogy a megfigyelés melyik tartományba esik (rang meghatározás). Amennyiben az összes esetet nézve, az összes ranghoz nagyjából azonos számú megfigyelés van hozzárendelve, akkor azt lehet mondani, hogy az ensemble jól reprezentálja az adott változó megfigyelt eloszlását.
Bondor Gyula
